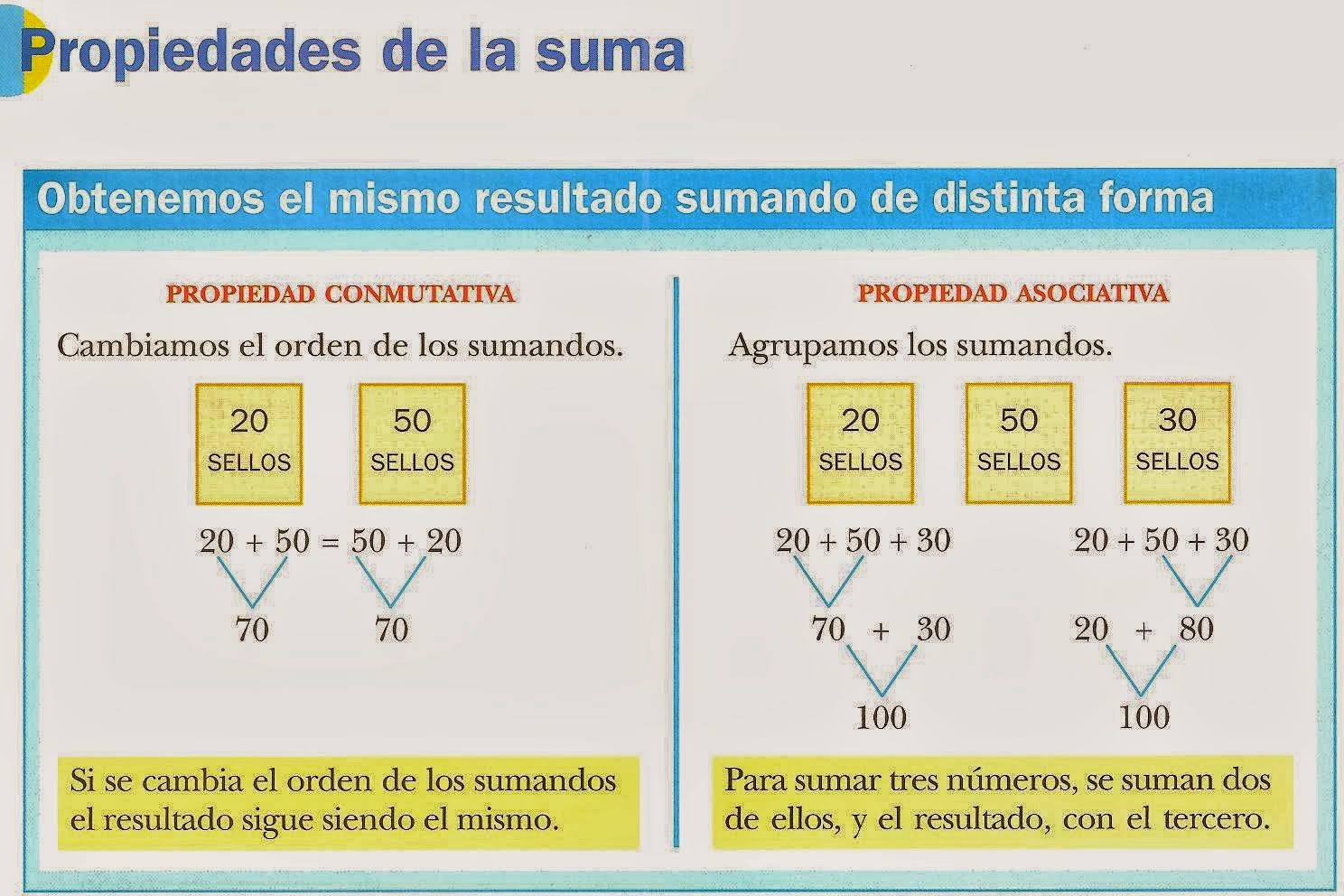
What are associative and commutative properties? And why are they important?
The associative property states that the grouping of operands in an expression does not affect the result. For example, (a + b) + c = a + (b + c). The commutative property states that the order of operands in an expression does not affect the result. For example, a + b = b + a.
These properties are important because they allow us to simplify expressions and perform calculations more efficiently. For example, we can use the associative property to group terms in an expression so that we can combine like terms. We can also use the commutative property to change the order of terms in an expression so that we can use a more efficient algorithm to calculate the result.
The associative and commutative properties are two of the most important properties of arithmetic operations. They are used extensively in mathematics and computer science.
Key Aspects of Associative and Commutative Properties
Associative and commutative properties are fundamental mathematical properties that govern the behavior of operations. They play a crucial role in simplifying expressions, performing calculations efficiently, and establishing algebraic structures.
- Operand Grouping
- Operand Order
- Expression Simplification
- Efficient Calculations
- Algebraic Structures
- Mathematical Foundations
These properties are closely intertwined, allowing for the manipulation and transformation of mathematical expressions. The associative property ensures that the grouping of operands does not alter the result, facilitating the rearrangement of terms for optimal evaluation. The commutative property, on the other hand, guarantees that the order of operands is inconsequential, enabling the interchange of terms without affecting the outcome. Together, these properties provide a solid foundation for algebraic operations and serve as building blocks for more complex mathematical concepts.
For instance, consider the expression (a + b) + c. Using the associative property, we can group the first two terms as a + (b + c), which is equivalent to the original expression. Similarly, the commutative property allows us to interchange the order of the first two terms, resulting in (b + a) + c, which again yields the same result. These properties streamline calculations, enhance problem-solving techniques, and contribute to the overall elegance and coherence of mathematical operations.
Operand Grouping
Operand grouping refers to the way in which operands (numbers or variables) are grouped together in a mathematical expression. The associative property states that the grouping of operands does not affect the result of an expression. For example, (a + b) + c is equivalent to a + (b + c). This property allows us to group operands in a way that makes the expression easier to evaluate.
- Order of Operations
The order of operations is a set of rules that dictate the order in which mathematical operations are performed. The associative property allows us to group operands in a way that conforms to the order of operations. For example, in the expression 1 + 2 3, the multiplication operation is performed before the addition operation. However, if we group the operands as (1 + 2) 3, the addition operation is performed before the multiplication operation.
- Simplifying Expressions
The associative property can be used to simplify expressions by combining like terms. For example, the expression a + b + a + c can be simplified to 2a + b + c by grouping the like terms a and a together.
- Evaluating Expressions
The associative property can be used to evaluate expressions by grouping the operands in a way that makes the evaluation easier. For example, the expression (1 + 2) 3 can be evaluated more easily than the expression 1 + 2 3.
The associative property is a fundamental property of mathematical operations. It allows us to group operands in a way that makes expressions easier to evaluate and simplify. This property is essential for understanding and working with mathematical expressions.
Operand Order
Operand order refers to the sequence in which operands (numbers or variables) appear in a mathematical expression. The commutative property states that the order of operands does not affect the result of an expression. For example, a + b is equivalent to b + a. This property allows us to change the order of operands without affecting the outcome of the expression.
The commutative property is closely related to the associative property, which states that the grouping of operands does not affect the result of an expression. Together, these two properties allow us to manipulate mathematical expressions in a variety of ways without affecting the outcome. For example, we can use the commutative property to change the order of operands in an expression so that we can use a more efficient algorithm to calculate the result. We can also use the associative property to group operands in a way that makes the expression easier to evaluate.
The commutative property is an important property of mathematical operations. It allows us to change the order of operands without affecting the outcome of the expression. This property is essential for understanding and working with mathematical expressions.
Expression Simplification
Expression simplification is the process of transforming a mathematical expression into an equivalent expression that is simpler or easier to evaluate. The associative and commutative properties are two important properties that can be used to simplify expressions.
The associative property states that the grouping of operands does not affect the result of an expression. For example, (a + b) + c is equivalent to a + (b + c). This property can be used to simplify expressions by grouping terms in a way that makes it easier to combine like terms.
The commutative property states that the order of operands does not affect the result of an expression. For example, a + b is equivalent to b + a. This property can be used to simplify expressions by changing the order of terms in a way that makes it easier to evaluate the expression.
Expression simplification is an important skill in mathematics. It can be used to make expressions easier to evaluate, to solve equations, and to prove mathematical theorems.
Efficient Calculations
The associative and commutative properties are two mathematical properties that can be used to simplify expressions and perform calculations more efficiently. The associative property states that the grouping of operands does not affect the result of an expression. For example, (a + b) + c is equivalent to a + (b + c). The commutative property states that the order of operands does not affect the result of an expression. For example, a + b is equivalent to b + a.
- Combining Like Terms
The associative property can be used to combine like terms in an expression. For example, the expression 2x + 3x + 5x can be simplified to 10x using the associative property. This can make it easier to evaluate the expression.
- Factoring Expressions
The commutative property can be used to factor expressions. For example, the expression x^2 + 2xy + y^2 can be factored as (x + y)^2 using the commutative property. This can make it easier to solve equations involving the expression.
- Simplifying Radicals
The associative and commutative properties can be used to simplify radicals. For example, the expression sqrt(a^2 + b^2) can be simplified to sqrt(a^2) + sqrt(b^2) using the associative and commutative properties. This can make it easier to evaluate the expression.
- Solving Equations
The associative and commutative properties can be used to solve equations. For example, the equation x + 5 = 10 can be solved using the associative property to group the terms on the left-hand side of the equation: (x + 5) - 5 = 10 - 5, which simplifies to x = 5.
The associative and commutative properties are two powerful tools that can be used to simplify expressions and perform calculations more efficiently. These properties are essential for understanding and working with mathematical expressions.
Algebraic Structures
Algebraic structures are mathematical systems that consist of a set of elements and one or more operations on those elements. The associative and commutative properties are two important properties that can be defined for operations on algebraic structures. The associative property states that the grouping of operands does not affect the result of an operation. The commutative property states that the order of operands does not affect the result of an operation.
The associative and commutative properties are important for algebraic structures because they allow us to simplify expressions and perform calculations more efficiently. For example, the associative property allows us to group terms in an expression so that we can combine like terms. The commutative property allows us to change the order of terms in an expression so that we can use a more efficient algorithm to calculate the result.
The associative and commutative properties are also important for the development of algebraic theories. For example, the associative property is essential for the development of group theory, which is the study of algebraic structures that have a single associative operation. The commutative property is essential for the development of ring theory, which is the study of algebraic structures that have two associative operations, one of which is commutative.
In conclusion, the associative and commutative properties are two important properties that can be defined for operations on algebraic structures. These properties allow us to simplify expressions and perform calculations more efficiently. They are also essential for the development of algebraic theories.
Mathematical Foundations
The associative and commutative properties are two fundamental mathematical properties that underpin a wide range of mathematical concepts and applications. These properties provide the foundation for algebraic structures, such as groups, rings, and fields, and play a crucial role in simplifying expressions, performing efficient calculations, and establishing mathematical proofs.
- Algebraic Structures
The associative and commutative properties are essential for defining and understanding algebraic structures. For instance, the associative property is a defining characteristic of groups, which are algebraic structures with a single associative operation. Similarly, the commutative property is a defining characteristic of commutative rings, which are algebraic structures with two associative operations, one of which is commutative.
- Expression Simplification
The associative and commutative properties allow for the simplification of mathematical expressions. The associative property enables the grouping of terms in an expression, facilitating the combination of like terms. The commutative property allows for the interchange of terms, enabling the use of more efficient algorithms for expression evaluation.
- Efficient Calculations
The associative and commutative properties contribute to efficient calculations. The associative property allows for the rearrangement of operands in an expression, enabling the use of more efficient algorithms for calculation. The commutative property allows for the interchange of operands, facilitating the use of faster or more convenient calculation methods.
- Mathematical Proofs
The associative and commutative properties are instrumental in mathematical proofs. They enable the manipulation and transformation of expressions, allowing for the establishment of mathematical theorems and the verification of mathematical conjectures.
In summary, the associative and commutative properties are foundational to mathematical structures, expression simplification, efficient calculations, and mathematical proofs. Their importance lies in providing a framework for understanding and manipulating mathematical expressions, facilitating efficient computation, and establishing the rigor and validity of mathematical reasoning.
Frequently Asked Questions about Associative and Commutative Properties
This section addresses common questions and misconceptions surrounding the associative and commutative properties, providing clear and informative answers to enhance understanding.
Question 1: What is the associative property?The associative property states that the grouping of operands in a mathematical expression does not affect the result. In other words, changing the way operands are grouped within an expression will not alter its value.
Question 2: What is the commutative property?The commutative property states that the order of operands in a mathematical expression does not affect the result. In other words, changing the order of operands within an expression will not alter its value.
Question 3: How are the associative and commutative properties related?The associative and commutative properties are closely related. The associative property allows for the rearrangement of operands within an expression, while the commutative property allows for the interchange of operands. Together, these properties provide a framework for manipulating mathematical expressions.
Question 4: Why are the associative and commutative properties important?The associative and commutative properties are fundamental to mathematics. They enable the simplification of expressions, facilitate efficient calculations, and provide a foundation for algebraic structures and mathematical proofs.
Question 5: Can you provide an example of the associative property?Consider the expression (a + b) + c. Using the associative property, we can group the operands differently as a + (b + c), and the result remains the same.
Question 6: Can you provide an example of the commutative property?Consider the expression a + b. Using the commutative property, we can change the order of the operands to b + a, and the result remains the same.
In summary, the associative and commutative properties are essential mathematical properties that govern the behavior of operations. They allow for the manipulation and transformation of expressions, facilitating efficient calculations and providing a solid foundation for more complex mathematical concepts.
Transitioning to the next article section, we will explore the applications of the associative and commutative properties in various mathematical contexts.
Conclusion
The associative and commutative properties are fundamental mathematical properties that permeate various mathematical disciplines, from algebra to calculus. Their importance lies in their ability to simplify expressions, facilitate efficient calculations, and provide a solid foundation for algebraic structures and mathematical proofs. By understanding and applying these properties, we gain a deeper appreciation for the rigor and elegance of mathematical reasoning.
As we delve deeper into the world of mathematics, we will encounter numerous applications of the associative and commutative properties. These properties serve as foundational principles that underpin complex mathematical theories and practical applications. Their significance extends beyond theoretical mathematics, as they find use in diverse fields such as computer science, engineering, and finance.
The exploration of the associative and commutative properties has illuminated their crucial role in mathematical operations and structures. These properties provide a framework for understanding and manipulating mathematical expressions, enabling efficient calculations, and establishing the validity of mathematical proofs. By embracing these properties, we not only enhance our mathematical prowess but also gain a deeper appreciation for the beauty and power of mathematics.
You Might Also Like
The Ultimate Guide To Navigating The Azure PortalDiscover Affordable MDF Board Prices Today!
Can A Legal Adult Date An Almost-Adult? The Age Of Consent Quandary
The Ultimate Guide To The Oceanic Climate And Deciduous Forest
Redness At Its Finest: Unlocking The Secrets Of The Red One Red Arrows
Article Recommendations