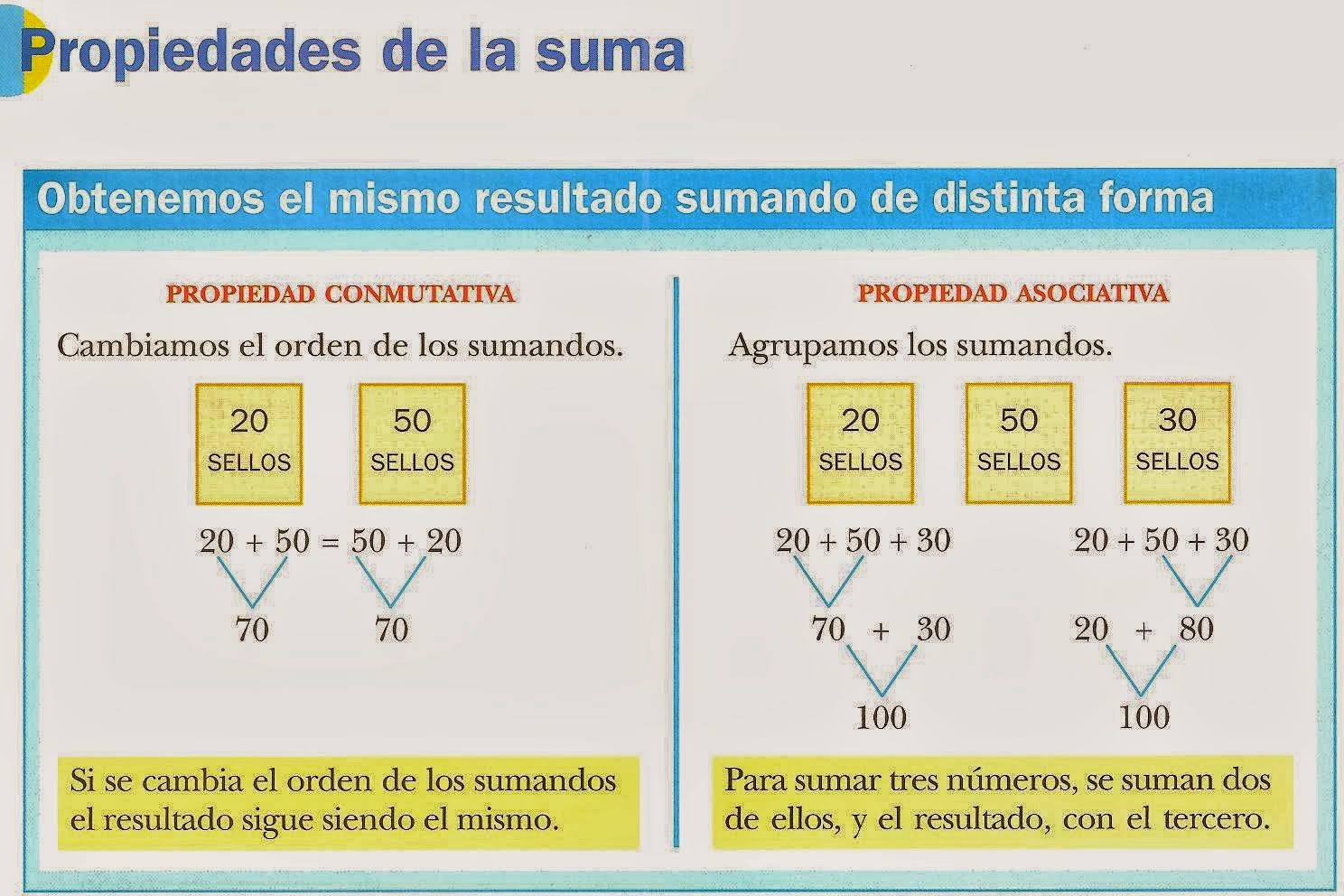
What are examples of commutative and associative properties?
The commutative property states that the order of operands in a mathematical operation does not affect the result. For example, 2 + 3 = 3 + 2. The associative property states that the way in which parentheses are placed in a mathematical expression does not affect the result. For example, (2 + 3) + 4 = 2 + (3 + 4).
These properties are important because they allow us to simplify mathematical expressions and make them easier to solve. For example, we can use the commutative property to rewrite 3 + 4 + 5 as 3 + 5 + 4, which is easier to add. We can use the associative property to rewrite ((2 + 3) + 4) + 5 as 2 + ((3 + 4) + 5), which is also easier to add.
The commutative and associative properties are two of the most basic properties of mathematics. They are used in a wide variety of mathematical applications, from simple arithmetic to complex algebra.
Key aspects of "ejemplos de propiedad conmutativa y asociativa"
The commutative and associative properties are two of the most basic properties of mathematics. They are used in a wide variety of mathematical applications, from simple arithmetic to complex algebra.
- Definition: The commutative property states that the order of operands in a mathematical operation does not affect the result. The associative property states that the way in which parentheses are placed in a mathematical expression does not affect the result.
- Examples: 2 + 3 = 3 + 2 (commutative property); (2 + 3) + 4 = 2 + (3 + 4) (associative property)
- Importance: These properties allow us to simplify mathematical expressions and make them easier to solve.
- Applications: The commutative and associative properties are used in a wide variety of mathematical applications, from simple arithmetic to complex algebra.
- History: The commutative and associative properties were first discovered by mathematicians in the 19th century.
- Connections: The commutative and associative properties are related to other mathematical properties, such as the distributive property.
In conclusion, the commutative and associative properties are two of the most important properties of mathematics. They are used in a wide variety of mathematical applications and allow us to simplify mathematical expressions and make them easier to solve.
Definition
The commutative and associative properties are two of the most basic properties of mathematics. They are used in a wide variety of mathematical applications, from simple arithmetic to complex algebra.
- Components: The commutative property has two components: the order of the operands and the result of the operation. The associative property has three components: the way in which the parentheses are placed, the order of the operations, and the result of the expression.
- Examples: The commutative property can be seen in the following examples: 2 + 3 = 3 + 2, 4 - 1 = 1 - 4, and 5 6 = 6 5. The associative property can be seen in the following examples: (2 + 3) + 4 = 2 + (3 + 4), (4 - 1) - 2 = 4 - (1 - 2), and (5 6) 7 = 5 (6 7).
- Implications: The commutative and associative properties have a number of implications in mathematics. For example, they allow us to simplify mathematical expressions and make them easier to solve. They also allow us to develop new mathematical formulas and theorems.
In conclusion, the commutative and associative properties are two of the most important properties of mathematics. They are used in a wide variety of mathematical applications and have a number of implications in mathematics.
Examples
The examples 2 + 3 = 3 + 2 and (2 + 3) + 4 = 2 + (3 + 4) are concrete illustrations of the commutative and associative properties, respectively. These properties are fundamental principles of mathematics that govern the order in which numbers can be combined in mathematical operations.
The commutative property states that the order of the operands in a mathematical operation does not affect the result. In other words, we can change the order of the numbers being added or multiplied without changing the answer. This property is essential for simplifying mathematical expressions and making them easier to solve. For example, we can use the commutative property to rewrite the expression 3 + 4 as 4 + 3, which is easier to add mentally.
The associative property states that the way in which parentheses are placed in a mathematical expression does not affect the result. In other words, we can group the numbers in different ways using parentheses without changing the answer. This property is essential for simplifying complex mathematical expressions and making them easier to solve. For example, we can use the associative property to rewrite the expression (2 + 3) + 4 as 2 + (3 + 4), which is easier to add.
The commutative and associative properties are two of the most important properties of mathematics. They allow us to simplify mathematical expressions, make them easier to solve, and develop new mathematical formulas and theorems.
Importance
The commutative and associative properties are two of the most important properties of mathematics. They allow us to simplify mathematical expressions and make them easier to solve. This is essential for a variety of mathematical applications, from simple arithmetic to complex algebra.
For example, the commutative property allows us to rewrite the expression 3 + 4 as 4 + 3, which is easier to add mentally. The associative property allows us to rewrite the expression (2 + 3) + 4 as 2 + (3 + 4), which is also easier to add.
These properties are also essential for developing new mathematical formulas and theorems. For example, the distributive property, which states that a(b + c) = ab + ac, can be derived from the commutative and associative properties.
In conclusion, the commutative and associative properties are two of the most important properties of mathematics. They allow us to simplify mathematical expressions, make them easier to solve, and develop new mathematical formulas and theorems.
Applications
The commutative and associative properties are two of the most important properties of mathematics. They are used in a wide variety of mathematical applications, from simple arithmetic to complex algebra.
- Simplification of expressions: The commutative and associative properties can be used to simplify mathematical expressions. For example, the expression 3 + 4 + 5 can be rewritten as 3 + (4 + 5) or (3 + 4) + 5. These equivalent expressions are easier to evaluate than the original expression.
- Solving equations: The commutative and associative properties can be used to solve equations. For example, the equation 3x + 4 = 10 can be rewritten as 3x = 10 - 4 or 3x = 6. These equivalent equations are easier to solve than the original equation.
- Development of mathematical formulas: The commutative and associative properties can be used to develop new mathematical formulas. For example, the distributive property, which states that a(b + c) = ab + ac, can be derived from the commutative and associative properties.
- Applications in computer science: The commutative and associative properties are used in a variety of computer science applications, such as compiler optimization and parallel computing.
The commutative and associative properties are essential for a variety of mathematical applications. They allow us to simplify expressions, solve equations, develop new formulas, and solve problems in computer science.
History
The discovery of the commutative and associative properties was a major milestone in the development of mathematics. These properties are now considered to be fundamental to mathematics, and they are used in a wide variety of mathematical applications.
- Impact on mathematics: The commutative and associative properties have had a profound impact on the development of mathematics. They have allowed mathematicians to develop new mathematical formulas and theorems, and they have also simplified the process of solving mathematical problems.
- Role in education: The commutative and associative properties are introduced to students in elementary school, and they continue to be used throughout their mathematical education. These properties are essential for understanding more advanced mathematical concepts, such as algebra and calculus.
- Applications in real life: The commutative and associative properties are used in a variety of real-life applications, such as computer science, engineering, and finance. For example, the associative property is used in computer science to design efficient algorithms, and the commutative property is used in finance to simplify the process of calculating interest.
The discovery of the commutative and associative properties was a major milestone in the development of mathematics. These properties are now considered to be fundamental to mathematics, and they are used in a wide variety of mathematical applications.
Connections
The commutative and associative properties are two of the most fundamental properties of mathematics. They are used in a wide variety of mathematical applications, from simple arithmetic to complex algebra.
- Distributive property: The distributive property states that a(b + c) = ab + ac. This property can be derived from the commutative and associative properties. For example, we can prove the distributive property as follows:
a(b + c) = a (c + b) [commutative property] = (a c) + (a * b) [associative property] = ab + ac
- Other properties: The commutative and associative properties are also related to other mathematical properties, such as the identity property, the zero property, and the inverse property. These properties form the foundation of elementary algebra and are essential for understanding more advanced mathematical concepts.
The commutative and associative properties are essential for a variety of mathematical applications. They allow us to simplify expressions, solve equations, develop new formulas, and solve problems in computer science and other fields.
Frequently Asked Questions about "ejemplos de propiedad conmutativa y asociativa"
This section provides answers to some of the most frequently asked questions about the commutative and associative properties in mathematics.
Question 1: What are the commutative and associative properties?
Answer: The commutative property states that the order of operands in a mathematical operation does not affect the result. The associative property states that the way in which parentheses are placed in a mathematical expression does not affect the result.
Question 2: Why are the commutative and associative properties important?
Answer: The commutative and associative properties are important because they allow us to simplify mathematical expressions and make them easier to solve. They also allow us to develop new mathematical formulas and theorems.
Question 3: Can you give some examples of the commutative and associative properties?
Answer: The commutative property can be seen in the following examples: 2 + 3 = 3 + 2, 4 - 1 = 1 - 4, and 5 6 = 6 5. The associative property can be seen in the following examples: (2 + 3) + 4 = 2 + (3 + 4), (4 - 1) - 2 = 4 - (1 - 2), and (5 6) 7 = 5 (6 7).
Question 4: How are the commutative and associative properties used in real life?
Answer: The commutative and associative properties are used in a variety of real-life applications, such as computer science, engineering, and finance. For example, the associative property is used in computer science to design efficient algorithms, and the commutative property is used in finance to simplify the process of calculating interest.
Question 5: What are some other mathematical properties that are related to the commutative and associative properties?
Answer: The commutative and associative properties are related to other mathematical properties, such as the distributive property, the identity property, the zero property, and the inverse property. These properties form the foundation of elementary algebra and are essential for understanding more advanced mathematical concepts.
Question 6: How can I learn more about the commutative and associative properties?
Answer: There are a variety of resources available to learn more about the commutative and associative properties. You can find books, articles, and videos on these topics online and in your local library. You can also ask your teacher or professor for help.
Summary: The commutative and associative properties are two of the most fundamental properties of mathematics. They are used in a wide variety of mathematical applications, from simple arithmetic to complex algebra. These properties allow us to simplify expressions, solve equations, develop new formulas, and solve problems in computer science and other fields.
Transition to the next article section: The commutative and associative properties are essential for understanding mathematics. In the next section, we will discuss some of the applications of these properties in real life.
Conclusion
The commutative and associative properties are two of the most fundamental properties of mathematics. They are used in a wide variety of mathematical applications, from simple arithmetic to complex algebra. These properties allow us to simplify expressions, solve equations, develop new formulas, and solve problems in computer science and other fields.
The commutative and associative properties are essential for understanding mathematics. They are used in every branch of mathematics, from algebra to calculus to number theory. These properties allow us to make sense of the world around us and to solve problems that we encounter in our everyday lives.
You Might Also Like
How Many Letters Are In The Alphabet Altogether?Complete Guide: Unveiling The Meaning Of "Beth" In Hebrew
Discover Etoh Abuse: A Comprehensive Guide To ICD-10 Codes
The Ultimate Guide: Understanding How Ubiquinol Functions In The Body
Expert Guide: Mount A Wood Block On Drywall With Ease
Article Recommendations